数据结构与算法(1.线性结构)

02 Aug 2022 in Posts / Algorithm

数据结构与算法(2.线性结构)

• 0. 前言
• 1. 线性表
• 2. 链表
  • 2.1 单向链表
  • 2.2 单向循环链表
  • 2.3 双向链表
  • 2.4 双向循环链表
• 3. 栈
  • 3.1 线性栈
  • 3.2 链式栈
• 4. 队列
  • 4.1 线性队列
  • 4.2 链式队列
• 5. 总结
  • 5.1 线性表
  • 5.2 链表
    • 5.2.1 单向链表
    • 5.2.2 单向循环链表
    • 5.2.3 双向链表
    • 5.2.4 双向循环链表
  • 5.3 栈
    • 5.3.1 线性栈
    • 5.3.2 链式栈
  • 5.4 队列
    • 5.4.1 线性队列
    • 5.4.2 链式队列

0. 前言

线性结构在存储结构上, 有以下2种:

• 顺序存储
• 链式存储

而多种逻辑结构皆可使用这2种存储结构实现.

顺序结构, 是在内存中开辟连续的空间存放数据, 再对数据进行操作, 有以下特性:

1. 存储空间大小固定, 从初始化时就被决定好了.
2. insert操作可能需要腾挪其他数据的位置.
3. delete操作可能要腾挪其他数据的位置.
4. get操作可通index直接获得.

链式存储, 是在内存中离散地存放数据, 再对数据进行操作, 有以下特性:

1. 存储空间大小不固定, 可灵活调整数据数量.
2. insert操作需要目标节点的previous和next一起操作指向.
3. delete操作需要目标节点的previous和next一起操作指向.
4. get操作需要通过遍历获取.

1. 线性表

• 存储结构: 连续存储.

例子: LinearList

归纳总结线性表:

1. 连续存储的存储结构使得部分高级语言无法手动指定实现
   1. 例如Python, 没有指针操作的存在, 导致无法手动开辟连续存储的内存空间
   2. C, C++, Objective-C, Swift等, 都能通过指针操作, 手动开辟连续的内存空间.
2. 开辟连续的存储空间, 有3个C/C++比较重要的开辟内存空间的函数, 理解他们可以让开辟内存空间的思路跟清晰.
   1. malloc, 仅仅开辟内存空间, 需要配合memset函数初始化内存空间数据.
   2. calloc, 开辟内存空间并初始化内存.
   3. realloc, 重新开辟内存空间, 并把原内存空间的内容拷贝到新的内存空间中, 并释放原内存空间.
3. 出于健壮性与语言特性的考虑, 表的空间大小需要进行管理与判断. 超出最大内存空间时, 可以通过重新开辟内存空间存放数据的方式来优化表, 即mutable.
4. 通过数据类型进行内存对齐后, get可以通过下标方式实现.
5. insert与delete需要遍历腾挪的内存空间
   1. insert由于需要往后挪位置, 所以需要从末尾开始遍历.
   2. delete由于需要往前挪位置, 所以可以从目标位置开始遍历.
6. clear只需要将length重置为0, 在开辟过的内存空间中的数据会被认为是无效数据.
7. 基于存储结构的reverse是通过首尾元素互换来实现的.

图解:

2. 链表

• 存储结构: 链式存储.

傻瓜式快速实现一个链表时, 会用到的一些归纳总结:

1. 有效节点的逻辑索引index总是从0开始.
2. 总是创建Header节点来标记首节点, 注意: 仅作标记作用.
3. 重点处理get和length方法, 能让逻辑更加清晰, 代码更加简单可读.
4. insert和delete操作可以总是通过index - 1的节点开始处理.
5. 基于链式结构的reverse是通过首插遍历法来实现的.

2.1 单向链表

例子: SinglyLinkedList

归纳总结单向链表: 离散排序的数据对象, 如按权重排序的数据表.

1. 可创建标记节点Header, Header的数据可以被额外利用为记录链表长度, 可以让获取链表长度的实现时间复杂度更少, 仅作标记用.
2. 出于健壮度的考虑, 实现一个链表的时候, 可以先实现length和empty方法. 为后面实现节点操作方法提供防止越界的判断方便.
3. 添加节点的方式有2种:
   1. 头插法, 新节点在Header节点后插入添加.
   2. 尾插法, 新节点在链表末尾插入, 通常这种方式更符合使用习惯.
4. get方法逐个遍历节点, 可被insert, delete, traverse方法方便使用, 在insert的时候, 由于需要处理index=0和index - 1的情况, 所以准入条件需要额外处理header.
5. insert, delete的规则是找到index-1位置再进行操作.
6. 删减方法的实现要注意语言的内存管理问题, 可能需要手动释放内存(如C、C++).

图解: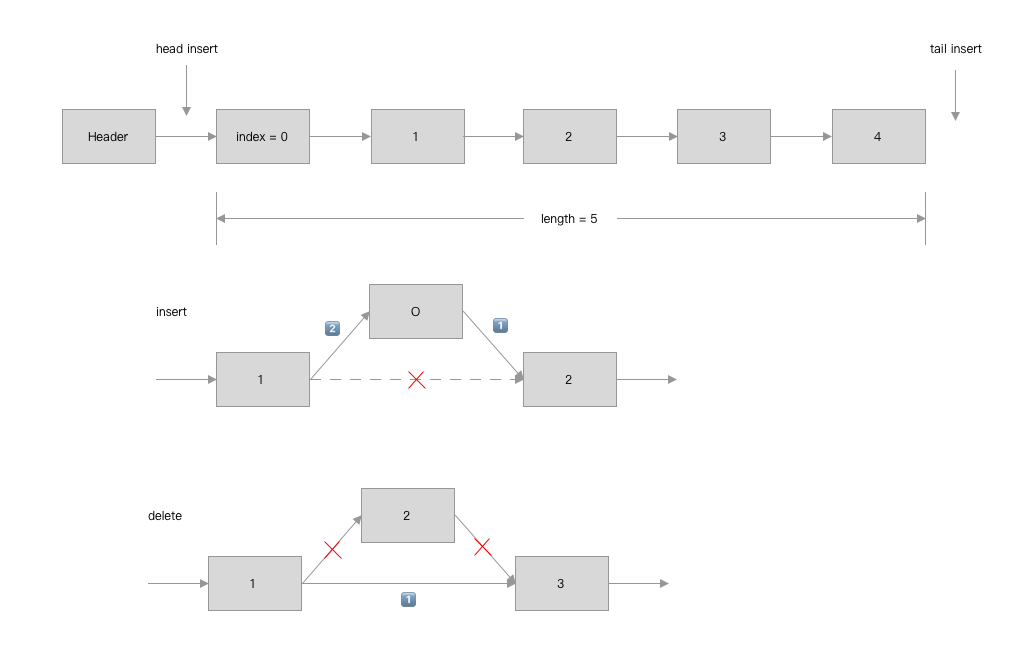

2.2 单向循环链表

例子: SinglyCircularLinkedList

使用场景: 扑克发牌流程.

归纳总结单项循环链表:

1. 因单向链表的操作都是从index-1位置开始操作index节点的, 所以单向循环列表需要特殊处理index=0的情况.
   1. insert, 要移动this->header->next = insertNode的指向.
   2. delete时, 要移动this->header->next = this->header->next->next的指向.
2. 在index = length时insert, 或add时, 与正常插入无区别.
3. 通过length来实现traverse或通过判断node->next == this->header->next来结束traverse循环.

图解: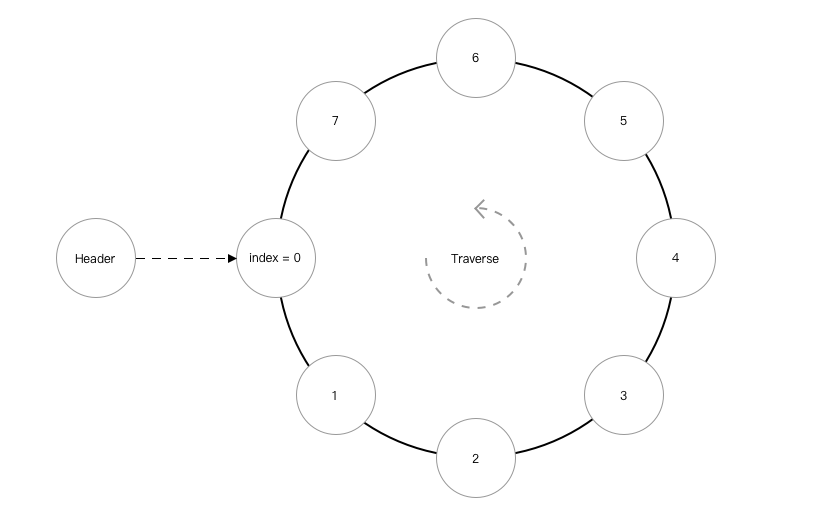

2.3 双向链表

例子: DoublyLinkedList

归纳总结双向链表:

1. 在单向链表的基础上节点添加了前驱节点的指针, 使得insert和delete时, 需要多处理previouse指针的指向.
2. 有previous和next的指针后, 节点的操作会变得更便捷.

图解: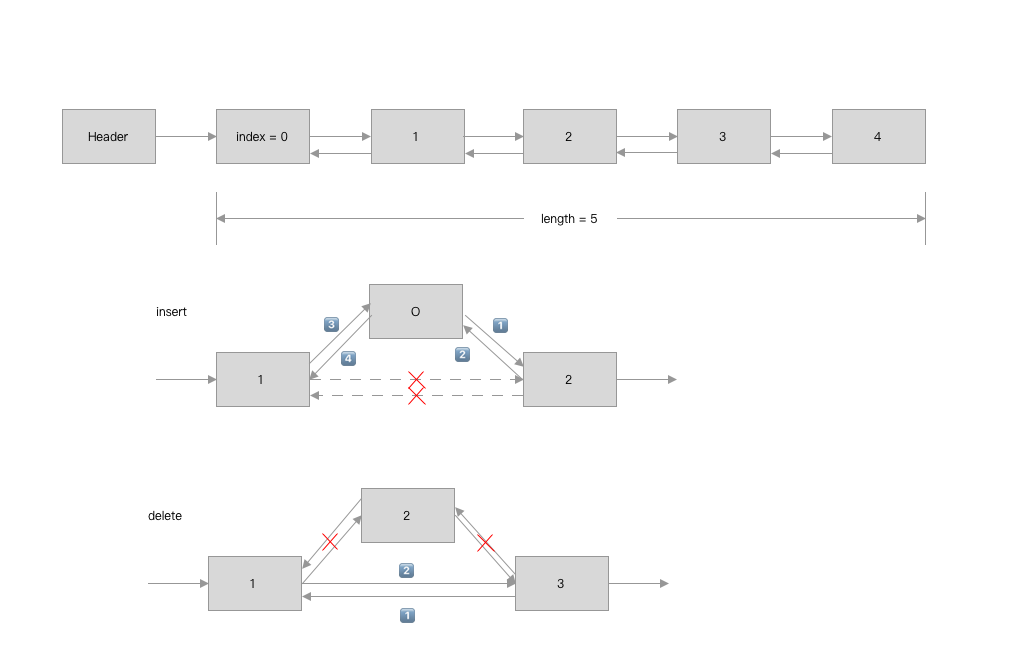

2.4 双向循环链表

例子: DoublyCircularLinkedList

归纳总结双向循环链表:

1. 注意index=0时的insert和delete.

图解: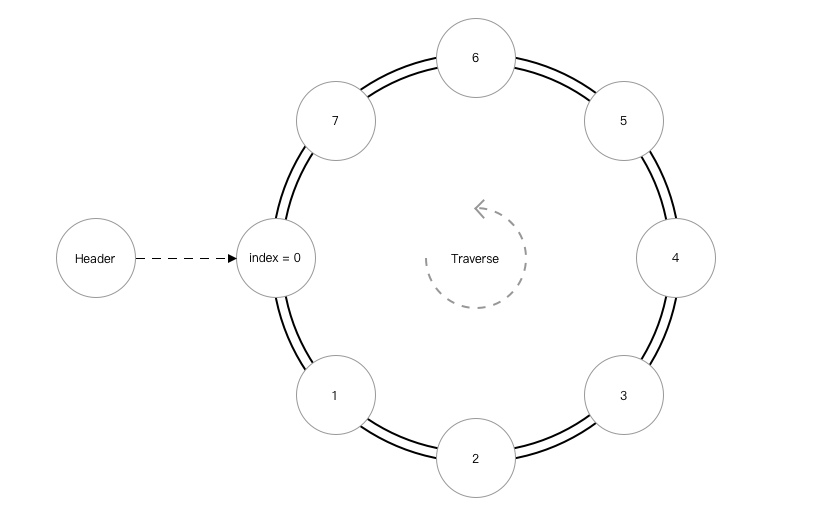

3. 栈

栈是一种操作受限的线性数据结构, 数据操作遵循先进后出的规则.

3.1 线性栈

例子: LinearStack

归纳总结线性栈:

1. 由于栈的特性是只能操作栈顶, 线性栈的数据操作无需挪移数据.
2. traverse操作是从栈顶往栈底的顺序进行.
3. clear操作只需要重置栈顶索引.
4. 初始化的top为-1, top + 1就是length

图解: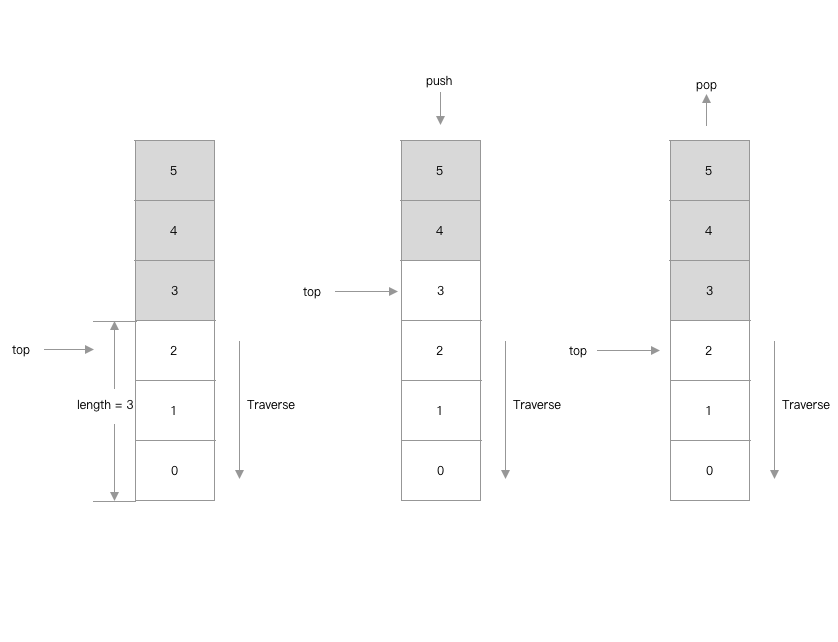

3.2 链式栈

例子: LinkedStack

归纳总结链式栈:

1. push操作其实就是头插法.
2. pop操作无需释放节点.

图解: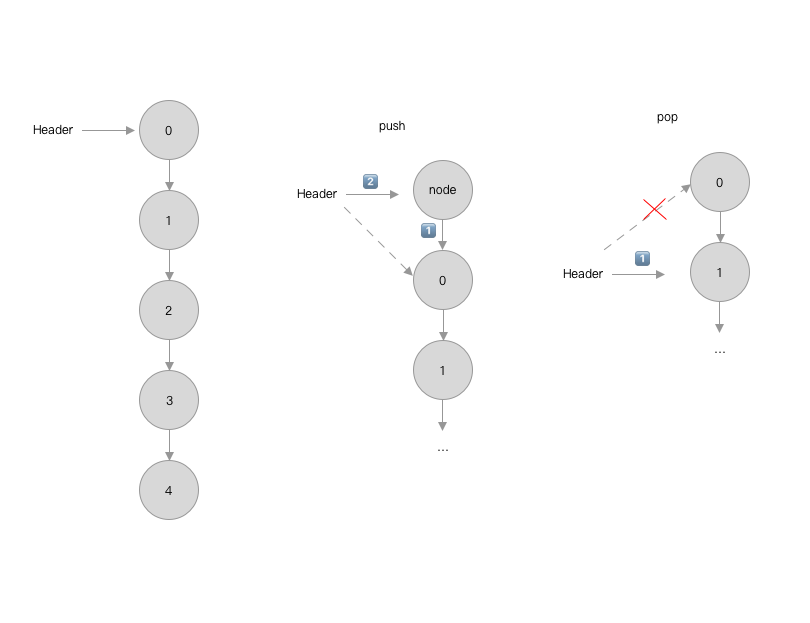

4. 队列

队列是一种操作受限的线性数据结构, 数据操作遵循先进先出的规则.

4.1 线性队列

例子: LinearQueue

归纳总结线性队列:

1. 数据最大数量固定, 且需要操作Header和Tailer, 所以可将线性队列看作一个循环
   1. Enqueue时, tailer = (tailer + 1) % capacity自增
   2. Dequeue时, header = (header + 1) % capacity自减
   3. Length时, (tailer - header + capacity) % capacity计算
2. 数据为空时, header == tailer
3. 数据为满时, (tailer + 1) % capacity == header, 从最大数据量中空出一个位置, 用于差异化满和空状态
4. 重置时, header = tailer = 0

图解: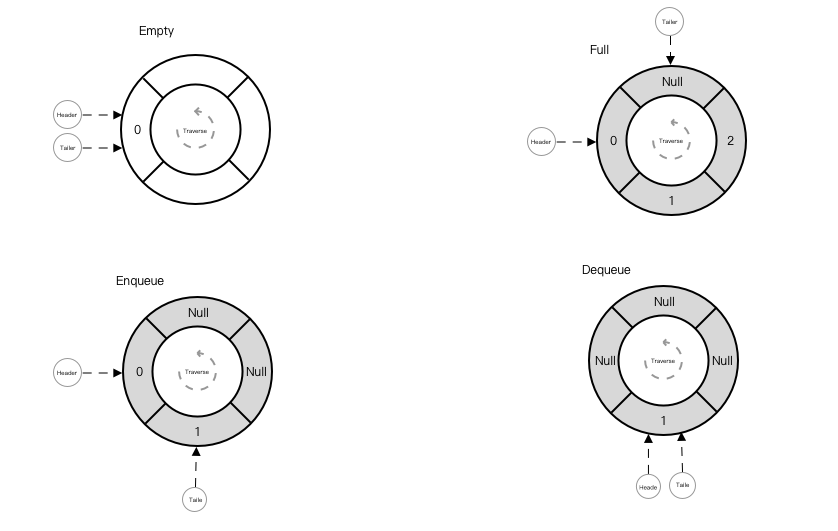

4.2 链式队列

例子: LinkedQueue

归纳总结链式队列:

1. 无节点数量限制
2. 使用尾插法时, header指向为空, 即为空队列
3. 得益于header和tailer的指向, Enqueue和Dequeue只需要操作首末数据的指向

图解: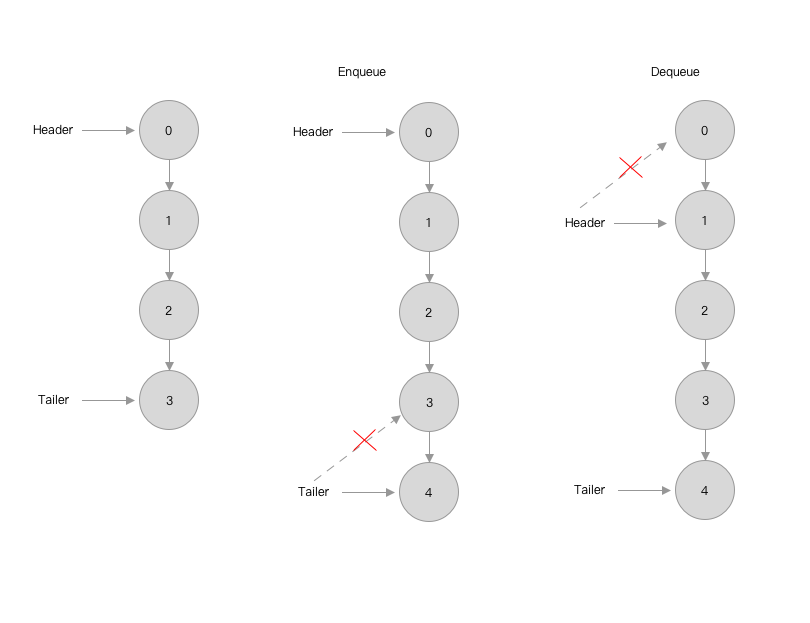

5. 总结

线性逻辑结构的特点是: 数据是1对1关系的

之后按照存储结构, 条件限制, 使用场景等情况, 衍生出了以下的实现.

5.1 线性表

特点:

1. 存储结构连续
2. 数据最大长度已知
3. 可通过索引直接获取数据
4. 数据插入删除涉及位置调整
5. 数据操作需要找到 index = n - 1 的数据节点进行操作

5.2 链表

特点:

1. 存储结构离散
2. 数据最大长度可变
3. 数据需要遍历获取
4. 数据的插入删除等操作, 需要依赖数据遍历
5. 总是利用Header节点能更容易实现链表的遍历

5.2.1 单向链表

特点:

1. 拥有5.2的特点
2. 数据遍历只能从首至末遍历

5.2.2 单向循环链表

特点:

1. 拥有5.2.1的特点
2. 限制: 末数据节点指向首数据节点
   1. 尾插法时, 注意指向首数据节点
   2. 头插法时(一般不使用), 注意末数据节点的指向

5.2.3 双向链表

特点:

1. 拥有5.2的特点
2. 数据可以双向遍历, 相当于增加了数据查找的方式

5.2.4 双向循环链表

特点:

1. 拥有5.2.3的特点
2. 限制: 末数据节点与首数据节点相互指向
   1. 尾插法时, 注意指向首数据节点

5.3 栈

特点:

1. 先入后出
2. 限制: 只能操作栈顶数据

5.3.1 线性栈

特点:

1. 拥有5.3的特点
2. 线性存储结构
3. 限制: 需要维护栈顶指针, 栈空时栈顶索引为< 0
4. 限制: 栈的最大长度固定, 栈满不可入栈

5.3.2 链式栈

特点:

1. 拥有5.3的特点
2. 离散存储结构
3. 限制: 使用链表的头插法入栈(出栈)

5.4 队列

特点:

1. 先进先出
2. 限制: 数据处理按照有序方式执行

5.4.1 线性队列

特点:

1. 拥有5.4的特点
2. 假溢出的情况, 需要让队尾预留一个节点的空间为空作为标记.
3. 存储空间大小固定.
4. 出入队列可以循环看待, 以%方式实现索引循环.

5.4.2 链式队列

特点:

1. 拥有5.4的特点
2. 存储空间大小无限制
3. header和tailer让Enqueue和Dequeue更便捷